Given that,
- $ n(H \cup E \cup P) = 74 $
- $ n( H \cap E \cap P) = 10 $
- $ n(H \cap E) = 20 $
- Only $ P = 0 $
We can draw the Venn diagram,
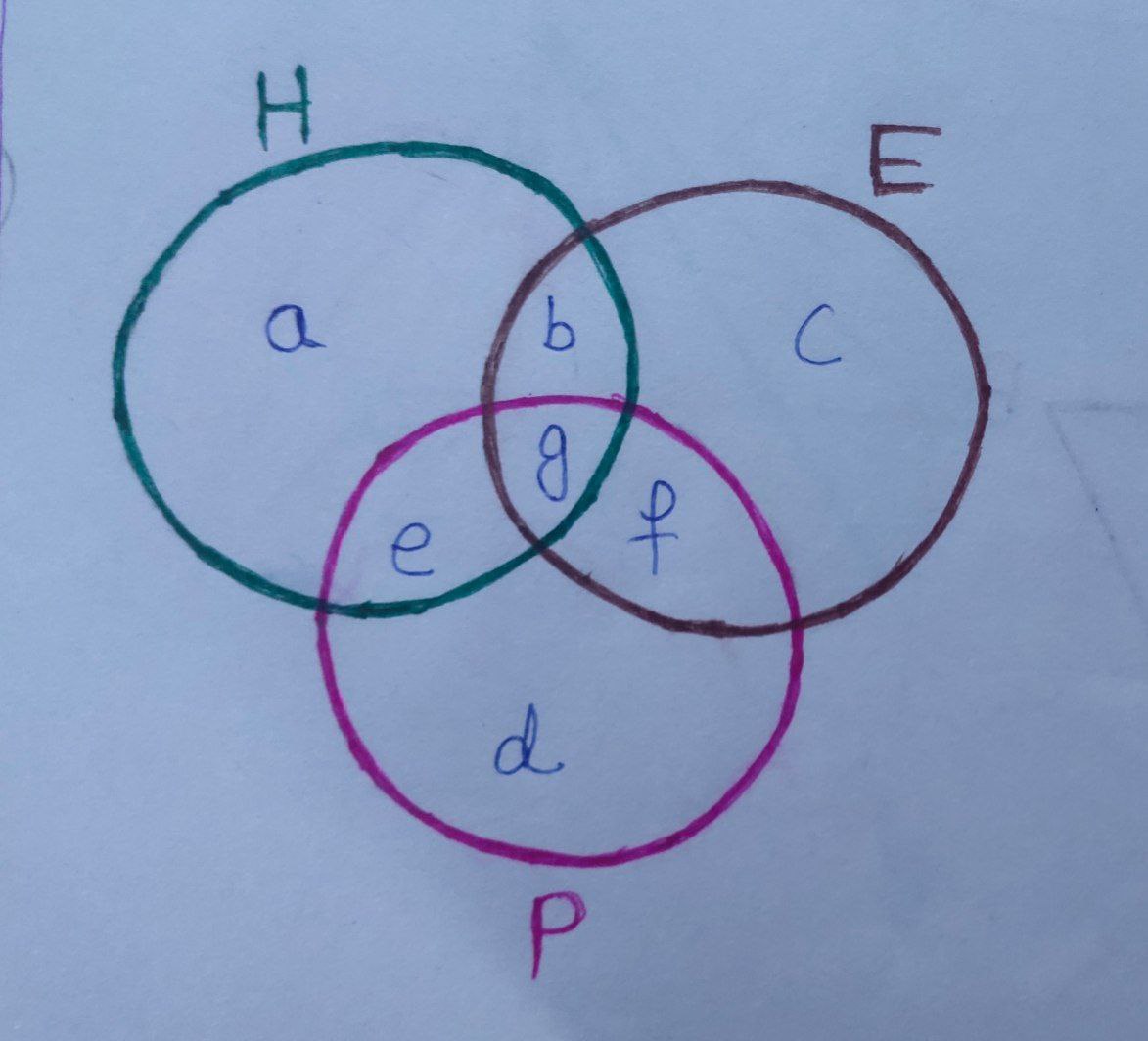
Here, given that $ : b=20, g=10, d=0 $
The number of students studying $ H = $ The number of students studying $E$
$ a + b + e + g = b + c + g + f $
$ \Rightarrow a + 20 + e + 10 = 20 + c + 10 + f $
$ \Rightarrow \boxed{a + e = c + f} \quad \longrightarrow (1) $
We have, $ a + b + c + d + e + f + g = 74 $
$ \Rightarrow a + 20 + c + 0 + e + f + 10 = 74 $
$ \Rightarrow a + e + c + f = 44 $
$ \Rightarrow 2(a+e) = 44 \quad [ \because \text{From equation (1)}]$
$ \Rightarrow \boxed{a + e = 22} $
$\therefore$ The number of students who studies $ H = a + b + e + g = 22 + 20 + 10 = 52.$
Correct Answer $: 52$