At a management school, the oldest $10$ dorms, numbered $1$ to $10$, need to be repaired urgently. The following diagram represents the estimated repair costs (in Rs. Crores) for the $10$ dorms. For any dorm, the estimated repair cost (in Rs. Crores) is an integer. Repairs with estimated cost Rs. $1$ or $2$ Crores are considered light repairs, repairs with estimated cost Rs. $3$ or $4$ are considered moderate repairs and repairs with estimated cost Rs. $5$ or $6$ Crores are considered extensive repairs.
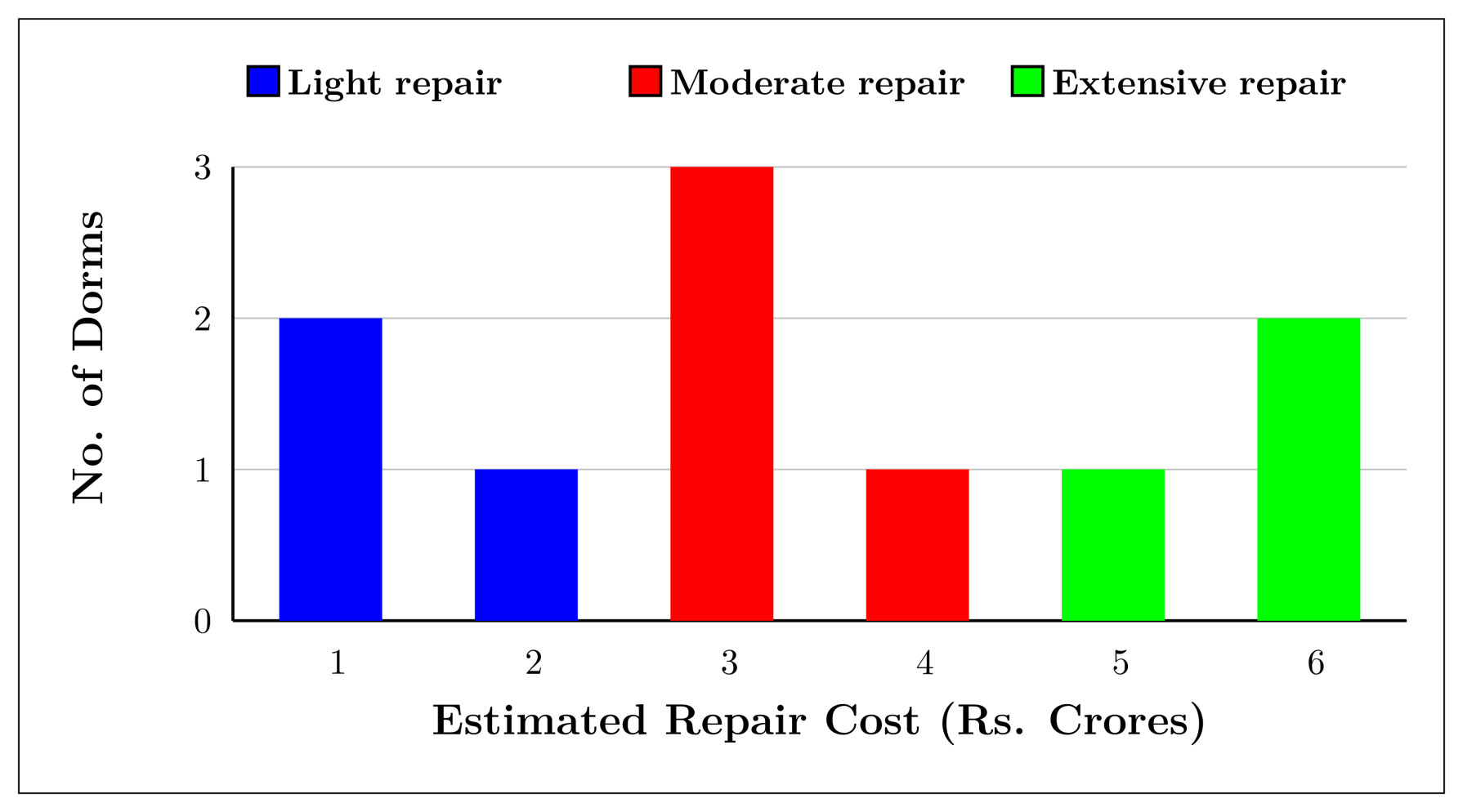
Further, the following are known:
- Odd-numbered dorms do not need light repair, even-numbered dorms do not need moderate repair and dorms, whose numbers are divisible by $3$, do not need extensive repair.
- Dorms $4$ to $9$ all need different repair costs, with Dorm $7$ needing the maximum and Dorm $8$ needing the minimum.
Which of the following is $\text{NOT}$ necessarily true?
- Dorm $1$ needs a moderate repair
- Dorm $5$ repair will cost no more than Rs. $4$ Crores
- Dorm $7$ needs an extensive repair
- Dorm $10$ repair will cost no more than Rs. $4$ Crores