At a management school, the oldest $10$ dorms, numbered $1$ to $10$, need to be repaired urgently, The following diagram represents the estimated repair costs (in Rs. Crores) for the $10$ dorms. For any dorm, the estimated repair cost (in Rs. Crores) is an integer. Repairs with estimated cost Rs. $1$ or $2$ Crores are considered light repairs, repairs with estimated cost Rs. $3$ or $4$ are considered moderate repairs and repairs with estimated cost Rs. $5$ or $6$ Crores are considered extensive repairs.
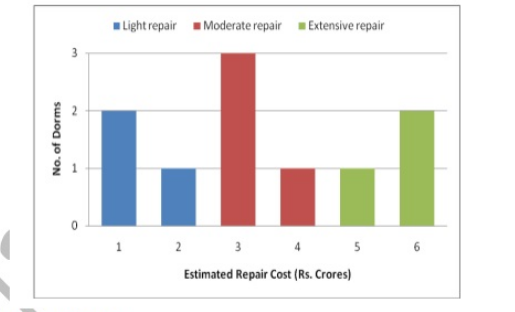
Further, the following are known:
- Odd-numbered dorms do not need light repair, even-numbered dorms do not need moderate repair and dorms, whose numbers are divisible by $3$, do not need extensive repair.
- Dorms $4$ to $9$ all need different repair costs, with Dorm $7$ needing the maximum and Dorm $8$ needing the minimum.
Suppose further that: $1.4$ of the $10$ dorms needing repair are women's dorms and need a total of Rs. $20$.Crores for repair $2$. Only one of Dorms $1$ to $5$ is a women's dorm.
What is the cost for repairing Dorm $9$ (in Rs. Crores)?
- $2$
- $12$
- $3$
- $4$