Let's draw the diagram for a better understanding.
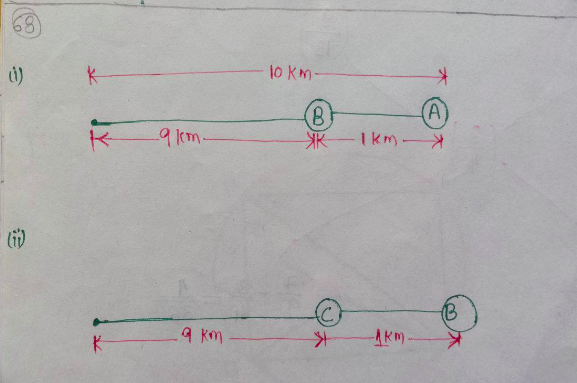
We know that, $\text{Speed} = \dfrac{\text{Distance}}{\text{Time}} $
If time is constant, then $\boxed{\text{Speed} \propto \text{Distance}}$
The ratio of the speed of $A$ and $B:$
The ratio of the speed of $B$ and $C:$
Now, we can combine the ratios.
- $S_{A}:S_{B} =(10:9)\times 10=100:90$
- $S_{B}:S_{C} =(10:9)\times 9=90:81$
$\Rightarrow S_{A}:S_{B}:S_{C} = 100:90:81$
We can write the ratio of Distance, $D_{A}:D_{B}: D_{C} = 10000 : 9000 : 8100.$
$\therefore \; A$ would beat $C$ by $1900$ meters.
Correct Answer $:\text{B}$