Let the distance from his home to his hostel be $D$ miles.
We know that, $\text{Time} = \dfrac{\text{Distance}}{\text{Speed}}$
Time has taken on his onward journey $T_{\text{onward}} = \frac{D}{60}$ hours
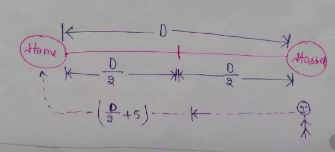
Time taken on his return journey $T_{\text{return}} = \left[\frac{\left(\frac{D}{2}\right)}{25}+\frac{\left(\frac{D}{2}+5\right)}{50}\right]$ hours
His return journey took $30$ minutes more than his onward journey.
That means, $T_{\text{return}} = T_{\text{onward}} + 30$ minutes
$\Rightarrow \frac{\frac{D}{2}}{25}+\frac{\frac{D}{2}+5}{50} = \frac{D}{60}+\frac{30}{60}$
$\Rightarrow \frac{D}{50}+\frac{D+10}{100} = \frac{D+30}{60}$
$\Rightarrow \frac{2D+D+10}{100} = \frac{D+30}{60}$
$\Rightarrow 3(3D+10) = 5(D+30)$
$\Rightarrow 9D+30 = 5D+150$
$\Rightarrow 4D = 120$
$\Rightarrow \boxed{D = 30\;\text{miles}}$
$\therefore$ The total distance traveled by him $ = D+\frac{D}{2}+\frac{D}{2}+5 = D+15+15+5 = 65$ miles.
Correct Answer $:\text{C}$