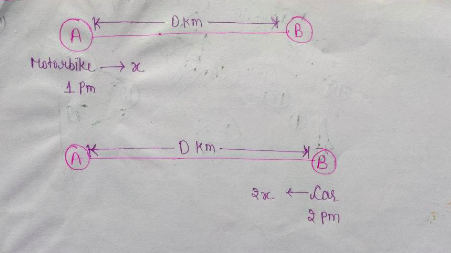
Let the distance between $A$ and $B$ be $D$ km, and the speed of the motorbike be $x$ km /hour. Then the speed of the car is $2x$ km/hour.
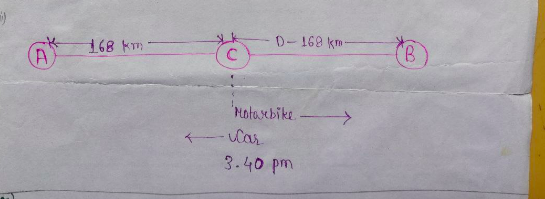
Let's say they met at point $C$.
We know that, $\text{Speed} = \dfrac{\text{Distance} }{\text{Time}}$
For motorbike:
$x = \dfrac{168}{\frac{8}{3}} \quad \left[\because 2 \;\text{hours}\; 40 \;\text{minutes} = 2 + \frac{40}{60} = 2 + \frac{2}{3} = \frac{8}{3} \;\text{hours}\right]$
$\Rightarrow \boxed{x = 63}$ km/hours
For car:
$2x = \dfrac{D-168}{\frac{5}{3}}$
$\Rightarrow2(63) = \dfrac{3(D-168)}{5} \quad \left[\because 1\;\text{hours}\; 40 \;\text{minutes} = 1 + \frac{40}{60} = 1 + \frac{2}{3} = \frac{5}{3}\;\text{hours} \right]$
$\Rightarrow 42\times5 = D-168$
$\Rightarrow 168 + 210 = D$
$\Rightarrow \boxed{D = 378\;\text{km}}$
$\therefore$ The distance between $A$ and $B$ is $378\;\text{km}.$
Correct Answer $:\text{B}$