Let's first draw the diagram.
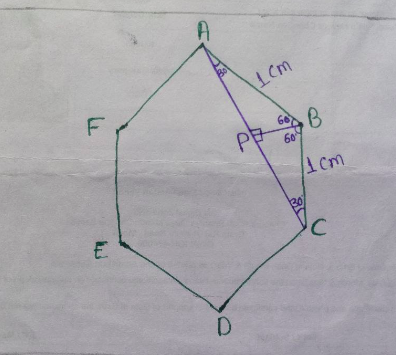
$\text{ABCDEF}$ is a regular hexagon.
So, each angle in the hexagon $= (\frac{n-2}{n})\times180^\circ$ , where $n=$number of sides
$\qquad \qquad = \left(\frac{6-2}{6}\right)\times180^\circ = \left(\frac{4}{6}\right)\times180^\circ = 120^\circ$
Now, $\frac{AP}{AB}= \cos 30^\circ$
$\Rightarrow \dfrac{\frac{AC}{2}}{1}=\frac{\sqrt{3}}{2}$
$\Rightarrow \frac{AC}{2}=\frac{\sqrt{3}}{2}$
$\Rightarrow \boxed{AC=\sqrt{3}\;\text{cm}}$
$\therefore$ The area of a square with $AC$ as one side$= (AC)^{2}= (\sqrt{3})^{2}=3\;\text{cm}^{2}.$
Correct Answer $:\text{B}$