Let's first draw the diagram.
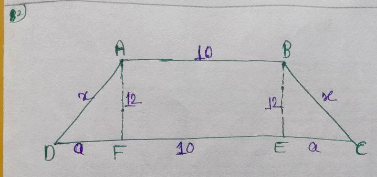
Let the length of the non-parallel side be $x$ cm.
Let $\text{DF} = \text{EC} = a\;\text{cm}.$
$\Rightarrow 2a = 20-10$
$\Rightarrow 2a = 10$
$\Rightarrow \boxed{a = 5\;\text{cm}}$
In $\triangle \text{AFD}$, apply the Pythagoras theorem
$(\text{AD})^{2} = (\text{AF})^{2}+(\text{DF})^{2}$
$\Rightarrow x^{2} = 12^{2}+5^{2}$
$\Rightarrow x^{2} = 144+125$
$\Rightarrow x^{2} = 169$
$\Rightarrow \boxed{x = 13\;\text{cm}}$
The diagram below represents the cross-section of the pillar.
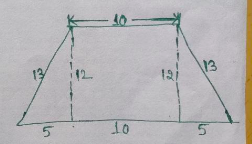
The total surface area of all the six surfaces $=$ Area of $4$ vertical surfaces with height $20$ cm and $2$ horizontal surfaces with the area as the area of trapezium.
$\qquad = \text{(Perimeter of the trapezium)} \times \text{Height of the pillar} + 2 \times \text{Area of trapezium}$
$\qquad = (10+13+20+13) \times 20+2\times\frac{1}{2}(10+20)\times12$
$\qquad = 56 \times 20 + 30 \times 12$
$\qquad = 1120 + 360$
$\qquad = 1480\;\text{ cm}^{2}$
$\therefore$ The total area, in sq cm, of all six surfaces of the pillar, is $1480.$
Correct Answer $:\text{C}$