We can draw the diagram for better understanding.
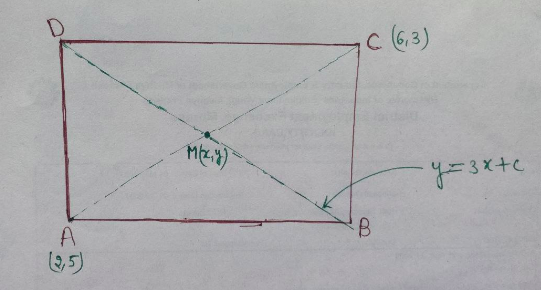
Let the midpoint of the rectangle be $M(x,y)$.
In a rectangle, diagonals bisect each other. So, one diagonal should pass through the midpoint of the other.
Midpoint $M(x,y)=M\left(\frac{2+6}{2},\frac{5+3}{2}\right) = M\left(\frac{8}{2},\frac{8}{2}\right) = M(4,4)$
The other diagonal, $y=3x+c$ should also pass through $(4,4):$
Now, $4 = 3(4) + c$
$\Rightarrow c = 4-12$
$\Rightarrow \boxed{c = -8}$
$\therefore$ The value of $c$ is $ -8.$
Correct Answer $:\text{D}$