Let's draw the diagram.
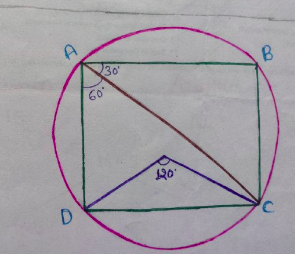
Now,
- $\angle COD=120^\circ, \angle BAC=30^\circ$
- $\angle DAC=\frac{\angle COD}{2}=\frac{120^\circ}{2}=60^\circ$
$\angle DAB=\angle DAC+\angle BAC$
$\Rightarrow\angle DAB=60^\circ+30^\circ=90^\circ$
The $ABCD$ is a cyclic quadrilateral, the sum of the opposite angles will be $180^\circ$.
$\Rightarrow \angle DAB+\angle BCD=180^\circ$
$\Rightarrow 90^\circ+\angle BCD=180^\circ$
$\Rightarrow \angle BCD=180^\circ-90^\circ$
$\Rightarrow \boxed{\angle BCD=90^\circ}$
Correct Answer $:\text{D}$