Let the one side be $L$ ft, and the other side be $B$ ft.
Let's draw the diagram for a better understanding.
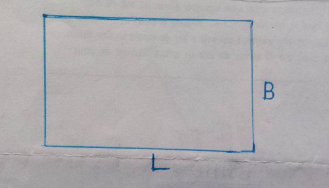
Given that, $L+2B=400$
$\Rightarrow 2B=400-L$
$\Rightarrow \boxed{B=\frac{(400-L)}{2}}$
Area of rectangle $A=L \ast B$
$\Rightarrow A=\frac{L\ast(400-L)}{2}$
$\Rightarrow A=200L-\frac{L^{2}}{2}$
The area is maximum when differentiation of $A$ is zero.
$\Rightarrow 200-\frac{2L}{2}=0$
$\Rightarrow 400-2L=0$
$\Rightarrow 2L=400$
$\Rightarrow \boxed{L=200\;\text{ft}}$
And, $B=\frac{400-200}{2}$
$\Rightarrow B = \frac{200}{2}$
$\Rightarrow\boxed{B = 100\;\text{ft}}$
$\therefore$ The length of the longer side is $200\;\text{ft}.$
Correct Answer $:\text{B}$