Let's first draw the diagram.
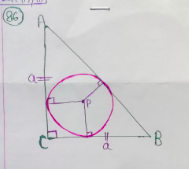
Let side $\text{AC} = \text{BC} = a\;\text{cm}.$
Here, $\text{P}$ is incenter.
In $ \triangle \text{ACB}$, apply the Pythagoras theorem.
$(\text{AB})^{2} = (\text{AC})^{2} + (\text{BC})^{2}$
$\Rightarrow (\text{AB})^{2} = (a)^{2} + (a)^{2}$
$\Rightarrow (\text{AB})^{2} = 2a^{2}$
$\Rightarrow \boxed{\text{AB} = a \sqrt{2}\;\text{cm}}$
In right angle triangle $\triangle \text{ABC}.$
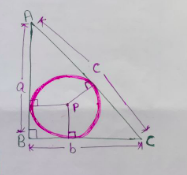
In radius of right angle triangle $ = \left(\frac{a+b-c}{2}\right)\;\text{cm}.$
Now, $\frac{a+a-a\sqrt2}{2} = 4(\sqrt2-1)$
$\Rightarrow \frac{2a-a\sqrt2}{2} = 4(\sqrt2-1)$
$\Rightarrow \frac{a}{2}(2-\sqrt2) = 4(\sqrt2-1)$
$\Rightarrow \frac{a}{\sqrt2}(\sqrt2-1) = 4(\sqrt2-1)$
$\Rightarrow \boxed{a = 4 \sqrt{2}\;\text{cm}}.$
$\therefore$ The area of $\triangle \text{ABC} = \frac{1}{2}\times \text{Base} \times \text{Height}$
$ \qquad \qquad = \frac{1}{2}\times a \times a = \frac{1}{2}\times a^{2} = \frac{1}{2}\times(4 \sqrt{2})^{2} = \frac{1}{2} \times 32 = 16\;\text{cm}^{2}.$
Correct Answer $:\text{A}$