Simple Happiness Index (SHI) of a country is computed on the basis of three parameters: social support (S), freedom to life choices (F) and corruption perception (C). Each of these three parameters is measured on a scale of $0$ to $8$ (Integers only). A country is then categorized based on the total score obtained by summing the score of the three parameters, as shown in the following table:
$\begin{array}{ccccc} \text{Total score} & 0-4 & 5-8 & 9-13 & 14-19 & 20-24 \\ \text{Category} & \text{Very Unhappy} & \text{Unhappy} & \text{Neutral} & \text{Happy} & \text{VeryHappy} \\ \end{array}$
Following diagram depicts the frequency distribution of the scores in S, F and C of $10$ countries – Amda, Benga, Calla, Delma, Eppa. Varsa, Wanna, Xanda, Yanga and Zooma;
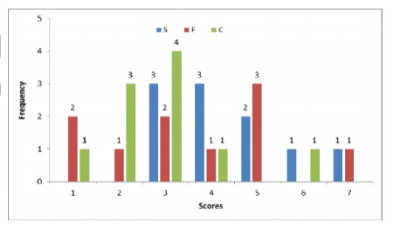
Further, the following are known:
1. Amda and Calls jointly have the lowest total score, $7$, with identical scores in all the three parameters.
2. Zooma has a total score of $17$.
3. All the $3$ countries, which are categorised as happy, have the highest score in exactly one parameter
Benga and Delma, two countries categorized as happy, are tied with the same total score. What is the maximum score they can have?
- $14$
- $15$
- $16$
- $17$