Simple Happiness Index (SHI) of a country is computed on the basis of three parameters: social support (S), freedom to life choices (F) and corruption perception (C). Each of these three parameters is measured on a scale of $0$ to $8$ (Integers only). A country is then categorized based on the total score obtained by summing the score of the three parameters, as shown in the following table:
$\begin{array}{ccccc} \text{Total score} & 0-4 & 5-8 & 9-13 & 14-19 & 20-24 \\ \text{Category} & \text{Very Unhappy} & \text{Unhappy} & \text{Neutral} & \text{Happy} & \text{VeryHappy} \\ \end{array}$
Following diagram depicts the frequency distribution of the scores in S, F and C of $10$ countries – Amda, Benga, Calla, Delma, Eppa. Varsa, Wanna, Xanda, Yanga and Zooma;
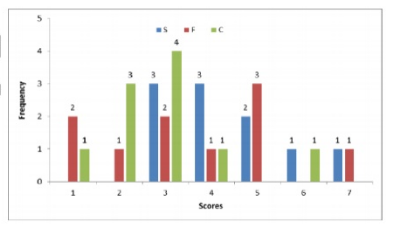
Further, the following are known:
1. Amda and Calls jointly have the lowest total score, $7$, with identical scores in all the three parameters.
2. Zooma has a total score of $17$.
3. All the $3$ countries, which are categorised as happy, have the highest score in exactly one parameter
If Benga scores $16$ and Delma scores $15$, then what is the maximum number of counties with a score of $13$?
- $0$
- $1$
- $2$
- $3$