We can draw the diagram.
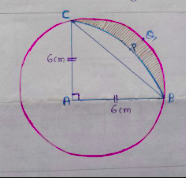
The $\triangle \text{CAB}$ is a right-angle triangle.
We can apply the Pythagorean theorem.
$\text{(BC)}^{2} = \text{(CA)}^{2} + \text{(AB)}^{2}$
$\Rightarrow \text{(BC)}^{2} = 6^{2} + 6^{2}$
$\Rightarrow \text{BC} = \sqrt{36 + 36} = \sqrt{72} = 6\sqrt{2}$
The required area $ = \text{area(BQC) – area(BPC)} = \underbrace{\text{area(BQC)}}_{\text{Semi-circle}} – [\;\underbrace{\text{area(ABPC)}}_{\text{Quarter circle}} – \underbrace{\text{area(ABC)}}_{\text{Triangle}}\;]$
Now, the area of semi-circle $\text{BQC:}$
- Radius of semi circle $\text{BQC}= \frac{BC}{2} = \frac{6\sqrt{2}}{2} = 3\sqrt{2}$ cm
- The area of semi circle $\text{BQC}= \frac{\pi}{2}(3\sqrt{2})^{2} = \frac{18\pi}{2}= 9\pi\;\text{cm}^{2}$
And, the area of quarter circle $\text{ABPC:}$
- Radius of quarter circle $\text{ABPC = AB = 6 cm}$
- The area of a quarter circle $\text{ABPC} = \frac{\pi}{4}(6)^{2}=9\pi \;\text{cm}^{2}$
The area of triangle $\text{ABC} = \frac{1}{2} \times 6 \times 6 = 18\;\text{cm}^{2}$
$\therefore$ The required area $= 9\pi-(9\pi-18)= 9\pi-9\pi-18 =18\;\text{cm}^{2}.$
Correct Answer $ : \text{B}$