Given that, $\text{ABCD}$ is a square and $\text{BCE}$ is an equilateral triangle.
Let the side of a square be $x$ cm.
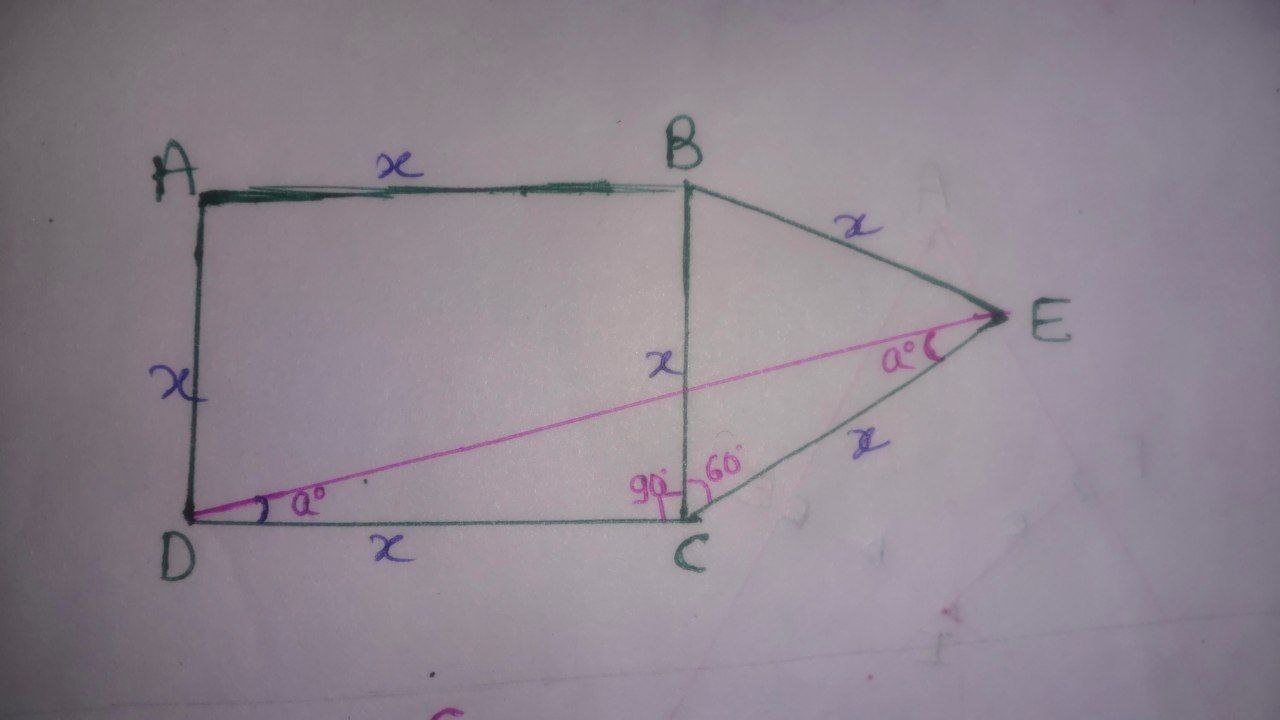
$\angle \text{BCD} = 90^{\circ}, \angle \text{BCE} = 60^{\circ}$
Then $\angle \text{DCE} = 90^{\circ}+60^{\circ} = 150^{\circ}$
Let $\angle \text{CDE} = \angle \text{DEC} = a^{\circ} \quad (\because \text{Angle opposite to the equal sides are equal})$
$\Rightarrow a + a+150^{\circ} = 180^{\circ}$
$\Rightarrow 2a = 30^{\circ}$
$\Rightarrow \boxed{a = 15^{\circ}}$
$\therefore \angle \text{DEC} = 15^{\circ}$
Correct Answer: $\text{A}$