First, we can draw the diagram.
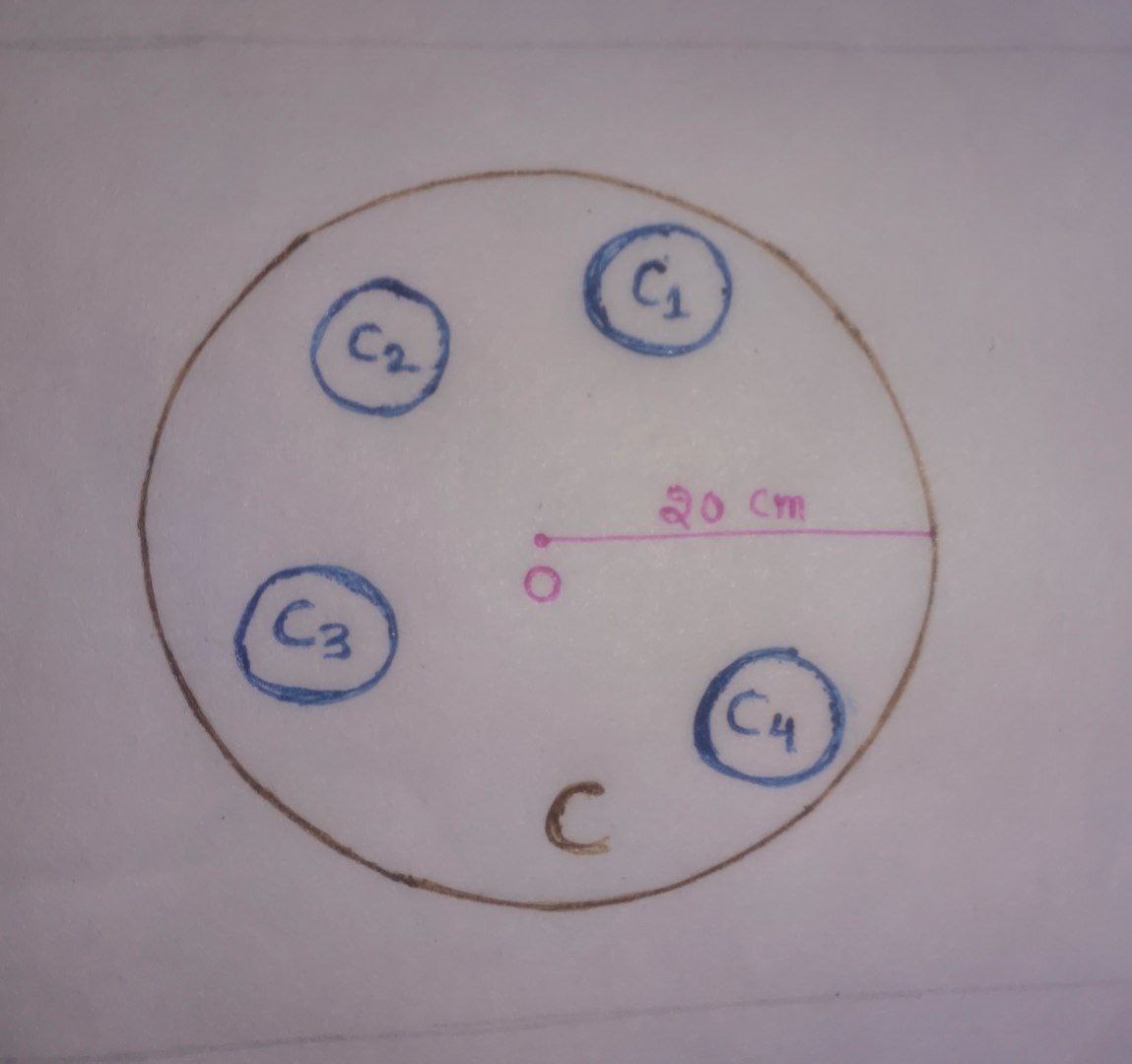
We know that area of circle $ = \pi \times(\text{radius})^{2}$
Four circles are cut from the circular sheet, each has a radius $ = 5\;\text{cm}$
Area of cut out portion $ = 4 \times \pi \times(5)^{2} = 4 \times \pi \times25 = 100 \pi$
Area of uncut portion $ = $ Area of circular sheet $-$ Area of a cutout portion
$\qquad \qquad \qquad \qquad= \pi \times(20)^{2}-100 \pi = 400 \pi -100 \pi = 300 \pi $
$\therefore$ The ratio of the uncut to the cut portion $ = 300 \pi :100 \pi = 3:1$
Correct Answer $:\text{C}$