Given that,
- $\text{AB}=2\ast6.5=13$ cm
- $\text{CA}=5$ cm
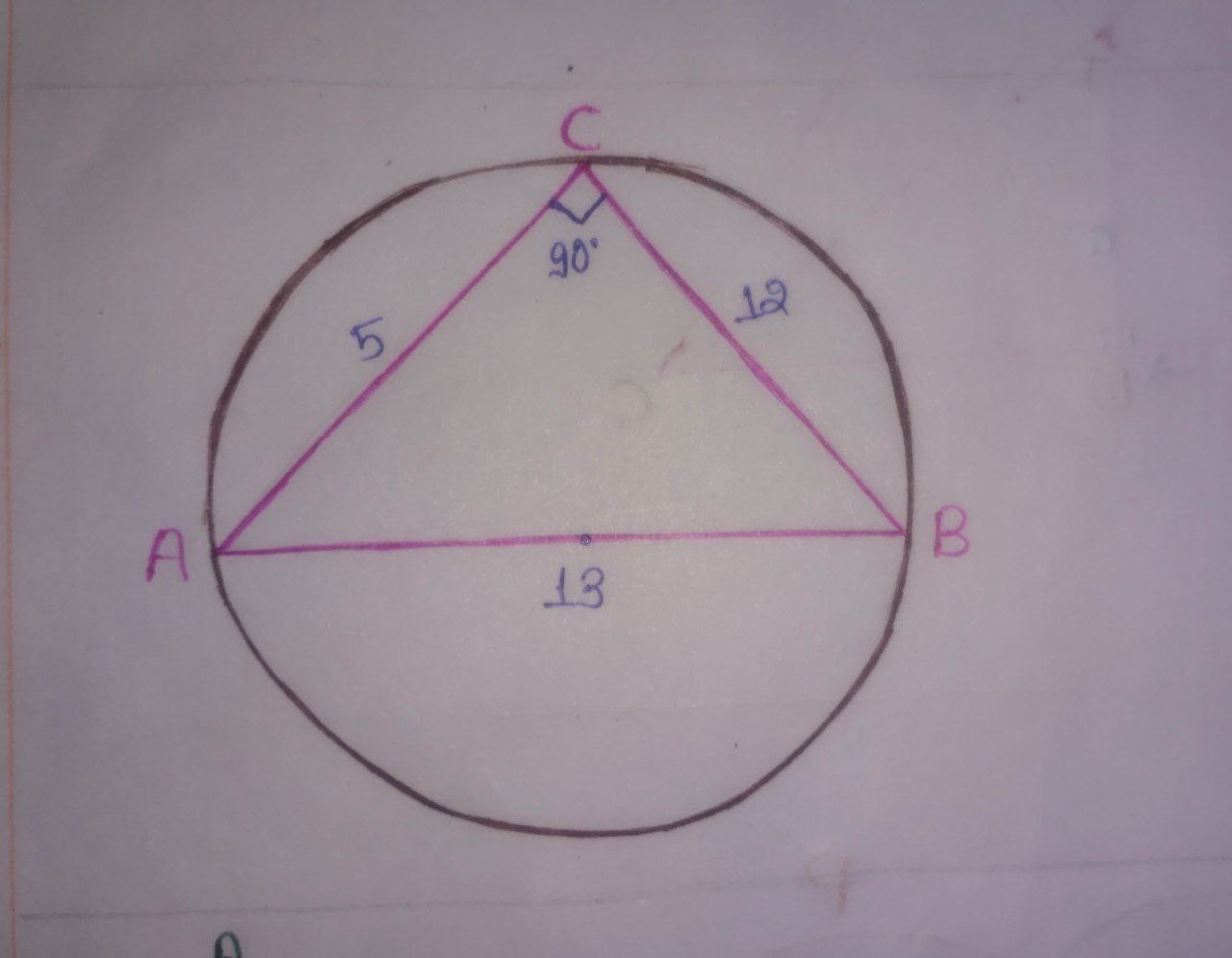
We know that, Angle in a semicircle is a right angle. So $\angle \text{ACB} = 90^\circ$.
Now, we can apply the Pythagorean theorem, in $\triangle \text{ACB}$.
$(\text{AB})^{2} = (\text{CA})^{2}+(\text{CB})^{2}$
$\Rightarrow (13)^{2} = (5)^{2}+(\text{CB})^{2}$
$\Rightarrow (\text{CB})^{2} = 169-25$
$\Rightarrow (\text{CB})^{2} = 144$
$\Rightarrow \boxed{\text{CB} = 12\;\text{cm}}$
$\therefore$ The area of $\triangle \text{ABC} = \frac{1}{2}\times \text{Base} \times \text{Height}$
$\qquad \qquad = \frac{1}{2}\times 5\times 12 = 30\; \text{cm}^{2}$
Correct Answer $:30$