Given that,
- $\text{AB} = 6$ cm
- $\text{BC} = 8$ cm
- $\angle \text{ABC} = 90^\circ$
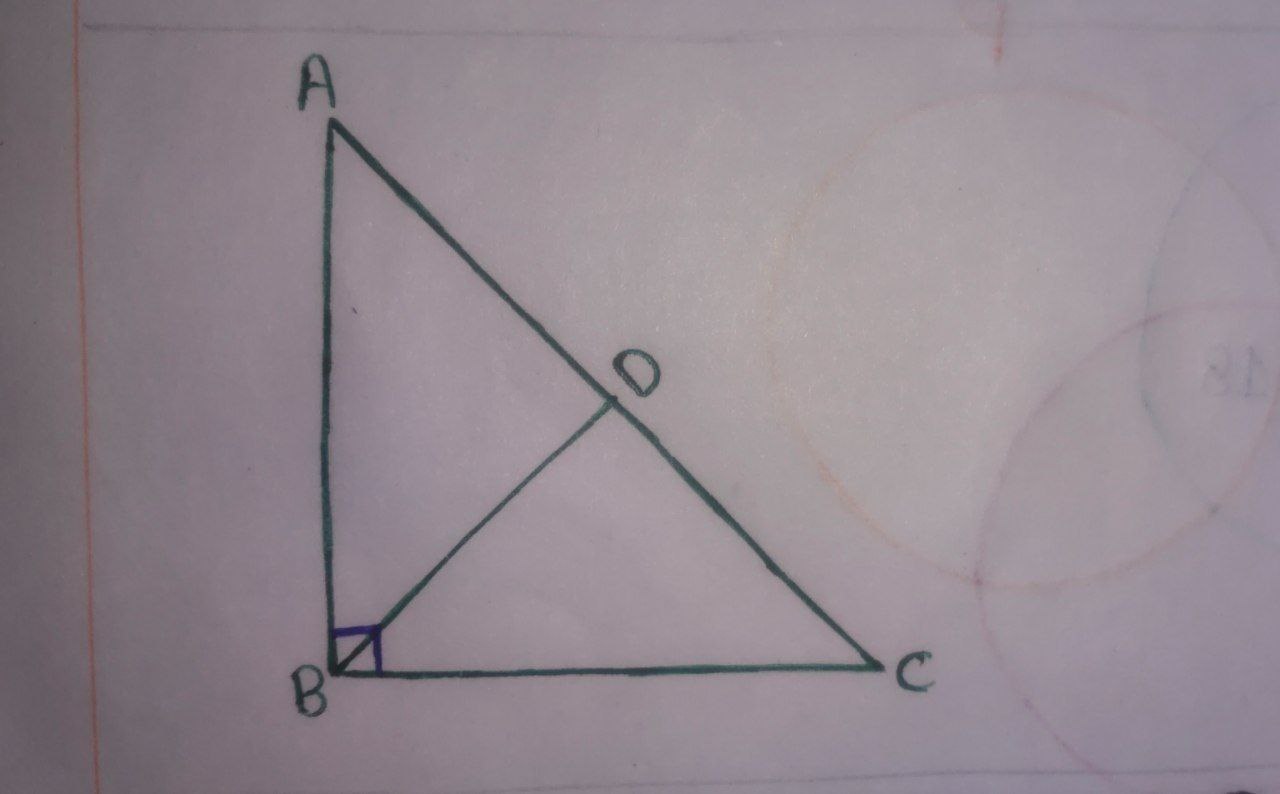
In $\triangle \text{ABC},$ we can apply the Pythagorean theorem.
$(\text{AC})^{2} = (\text{AB})^{2}+(\text{BC})^{2}$
$\Rightarrow (\text{AC})^{2} = 6^{2}+8^{2}$
$\Rightarrow (\text{AC})^{2} = 36+64$
$\Rightarrow (\text{AC})^{2} = 100$
$\Rightarrow \boxed{\text{AC} = 10\;\text{cm}}$
$\text{D}$ is the mid point of $\text{AC}$, thus $\text{AD = DC} = \frac{10}{2}=5$ cm
Also, $(\text{BD})^{2} = (\text{AD})\times(\text{DC})$
$\Rightarrow (\text{BD})^{2} = 5 \times 5 = 25$
$\Rightarrow \boxed{\text{BD} = 5\;\text{cm}}$
$\therefore$ The length of $\text{BD}$ is $5\;\text{cm}.$
Correct Answer $: 5$