CAT 2016 | Question: 86

Question

A man travels three-fifths of a distance $\text{AB}$ at a speed $3a$, and the remaining at a speed $2b$. If he goes from $\text{B}$ to $\text{A}$ and return at a speed $5c$ in the same time, then

• A. $1/a+1/b=1/c$
• B. $a+b=c$
• C. $1/a+1/b=2/c$
• D. $\text{None of these}$.

Answer 1

Let the distance $\text{AB}$ be $\text{D}$ km.

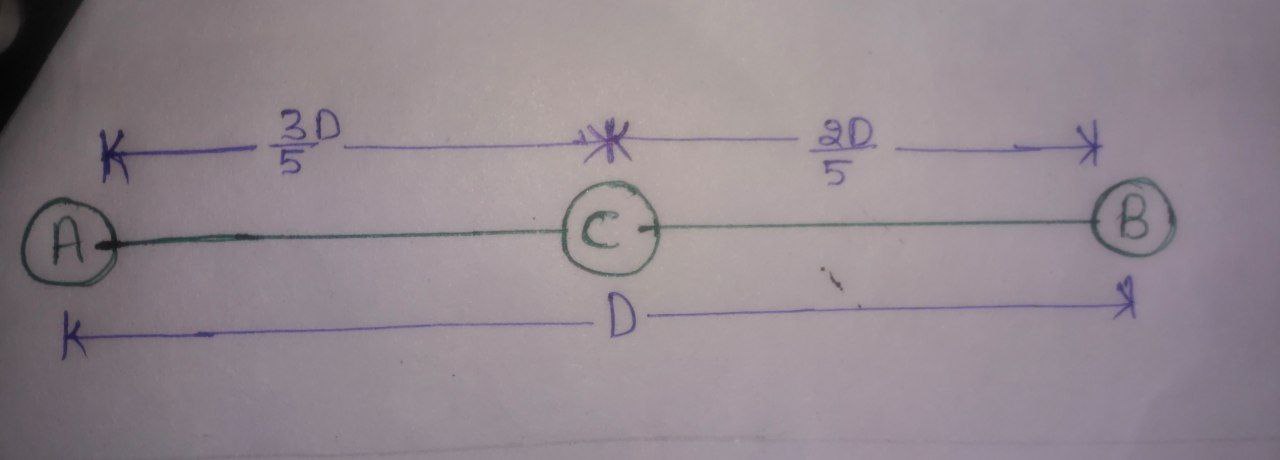
We know that, $\text{Speed} = \dfrac{\text{Distance} }{\text{Time}}$

• Time taken from $\text{A}$ to $\text{C : T}_{(\text{AC})} = \frac{\frac{3}{5}\text{D}}{3a} = \frac{3\text{D}}{5\times3a} = \frac{\text{D}}{5a}$ hr
• Time taken from $\text{C}$ to $\text{B : T}_{(\text{CB})} = \frac{\frac{2}{5}\text{D}}{2b} = \frac{2\text{D}}{5\times2b} = \frac{\text{D}}{5b}$ hr
• Time taken from $\text{B}$ to $\text{A}$, then $\text{A}$ to $\text{B : T}_{(\text{BA+AB})} = \frac{2\text{D}}{5c}$ hr

We have, $\text{T}_{(\text{AC})}+ \text{T}_{(\text{CB})} = \text{T}_{(\text{BA+AB})}$

$\Rightarrow \frac{\text{D}}{5a}+\frac{\text{D}}{5b} = \frac{2\text{D}}{5c}$

$\Rightarrow \require{cancel} \cancel{\frac{\text{D}}{5}} \left(\frac{1}{a}+\frac{1}{b}\right) = \cancel{\frac{\text{D}}{5}}\left(\frac{2}{c}\right)$

$\Rightarrow \boxed{\frac{1}{a}+\frac{1}{b} = \frac{2}{c}}$

Correct Answer $:\text{C}$