Given that, $x^{\frac{2}{3}}+x^{\frac{1}{3}}-2\leq0$
$\Rightarrow x^{\frac{1}{3}} \cdot x^{\frac{1}{3}} + x^{\frac{1}{3}} – 2\leq 0 \quad \longrightarrow (1)$
Let $x^{\frac{1}{3}} = k$
Now, $k \cdot k + k - 2\leq0$
$\Rightarrow k^{2} + k - 2\leq0$
$\Rightarrow k^{2} + 2k-k-2\leq0$
$\Rightarrow k(k+2)-1(k+2)\leq0$
$\Rightarrow (k+2)(k-1)\leq0$
$\Rightarrow \boxed{\left(x^{\frac{1}{3}}+2\right)\left(x^{\frac{1}{3}}-1\right)\leq 0} \quad \longrightarrow (2)$
$\textbf{Case 1:}\;x^{\frac{1}{3}}+2\leq0;$ $x^{\frac{1}{3}}-1\geq0$
$\Rightarrow x^{\frac{1}{3}}\leq-2;$ $x^{\frac{1}{3}}\geq1$
$\Rightarrow \boxed{x\leq-8; x\geq1}$
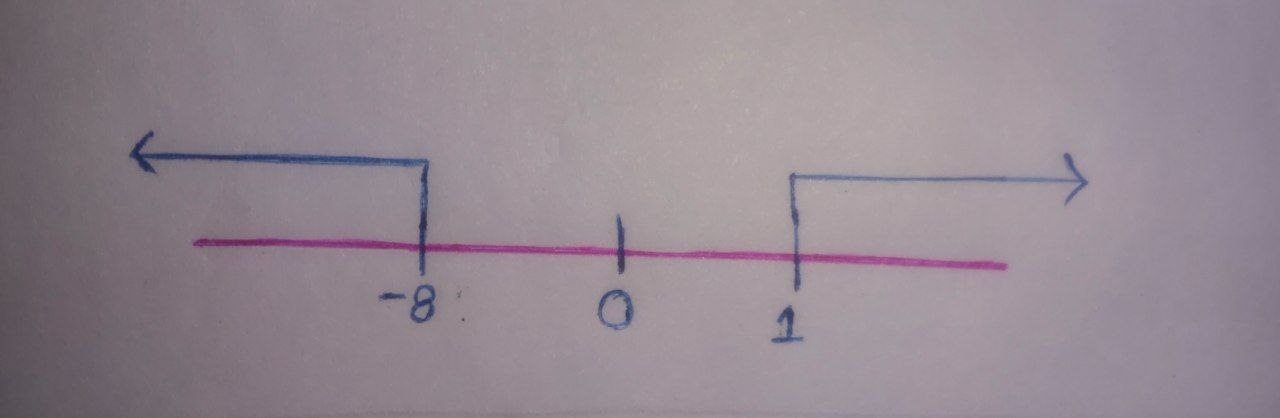
For $x$ solution is not possible.
$\textbf{Case 2:} \;x^{\frac{1}{3}}+2\geq0;$ $x^{\frac{1}{3}}-1\leq0$
$\Rightarrow x^{\frac{1}{3}}\geq-2;$ $x^{\frac{1}{3}}\leq1$
$\Rightarrow \boxed{x\geq-8; x\leq1}$
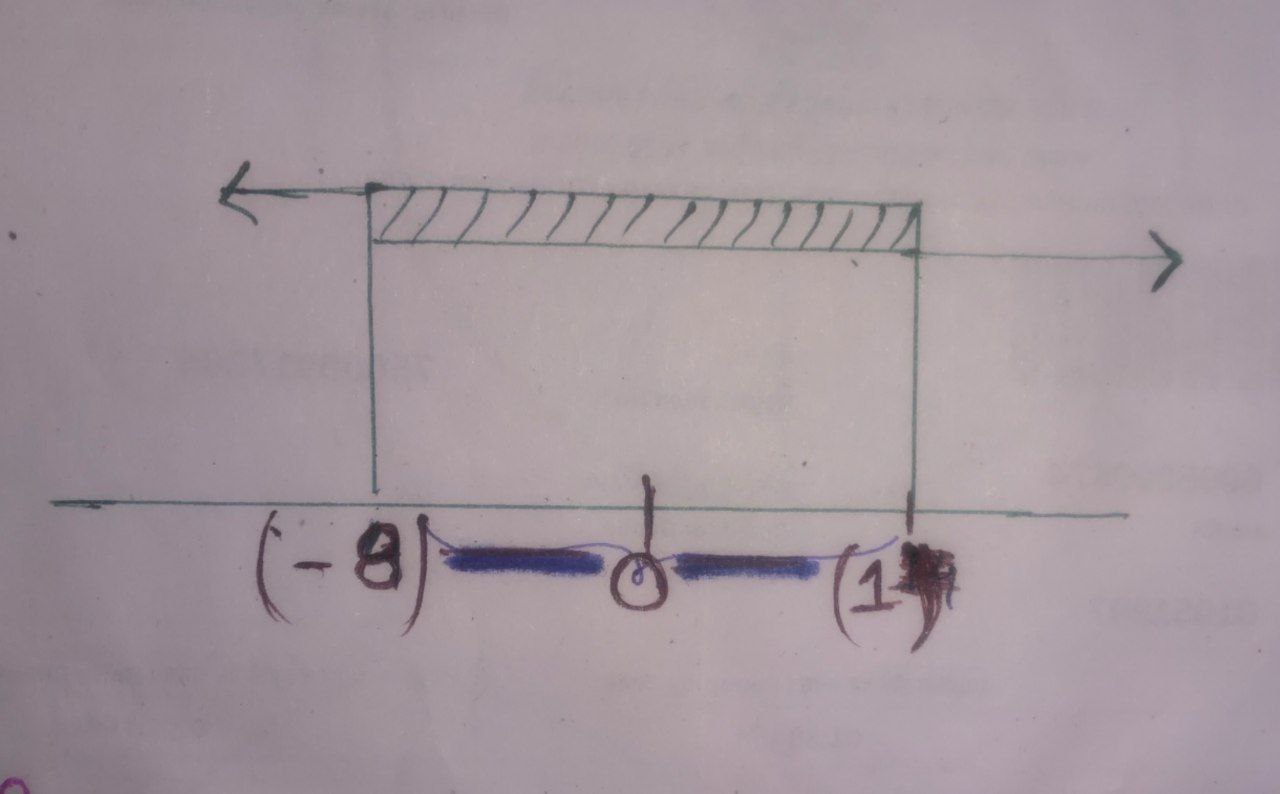
$\Rightarrow \boxed{-8\leq x\leq1}$
Correct Answer $:\text{A}$