Given that,
- $2x+3y-5=0 \longrightarrow(1)$
- $5x-7y+2=0 \longrightarrow(2)$
- $9x-5y-4=0 \longrightarrow(3)$
Take equation $(1)$ and $(2).$
$2x+3y-5=0 \longrightarrow(1)\times7$
$5x-7y+2=0 \longrightarrow(2)\times3$
$14x+21y-35=0$
$15x-21y+6=0$
----------------------------------
$29x-29=0$
$\boxed{x=1}$
Put the value of $’x’$ in equation $(1)$,we get.
$2(1)+3y-5=0$
$\Rightarrow 3y=3$
$\Rightarrow \boxed{y=1}$
Take equation $(1)$ and $(3).$
$2x+3y-5=0 \longrightarrow(1)\times5$
$9x-5y-4=0 \longrightarrow(3)\times3$
$10x+15y-25=0$
$27x-15y-12=0$
----------------------------------
$37x-37=0$
$\Rightarrow\boxed{x=1}$
Put the value of $’x’$ in equation $(3)$,we get.
$9(1)-5y-4=0$
$\Rightarrow -5y+5=0$
$\Rightarrow \boxed{y=1}$
Take equation $(2)$ and $(3).$
$5x-7y+2=0 \longrightarrow(2)\times5$
$9x-5y-4=0 \longrightarrow(3)\times7$
$25x-35y+10=0$
$63x-35y-28=0$
----------------------------------
$-38x+38=0$
$\Rightarrow\boxed{x=1}$
Put the value of $’x’$ in equation $(2)$,we get.
$5(1)-7y+2=0$
$\Rightarrow -7y+7=0$
$\Rightarrow \boxed{y=1}$
We can say that, these three lines meet at point $M(x,y)=M(1,1).$
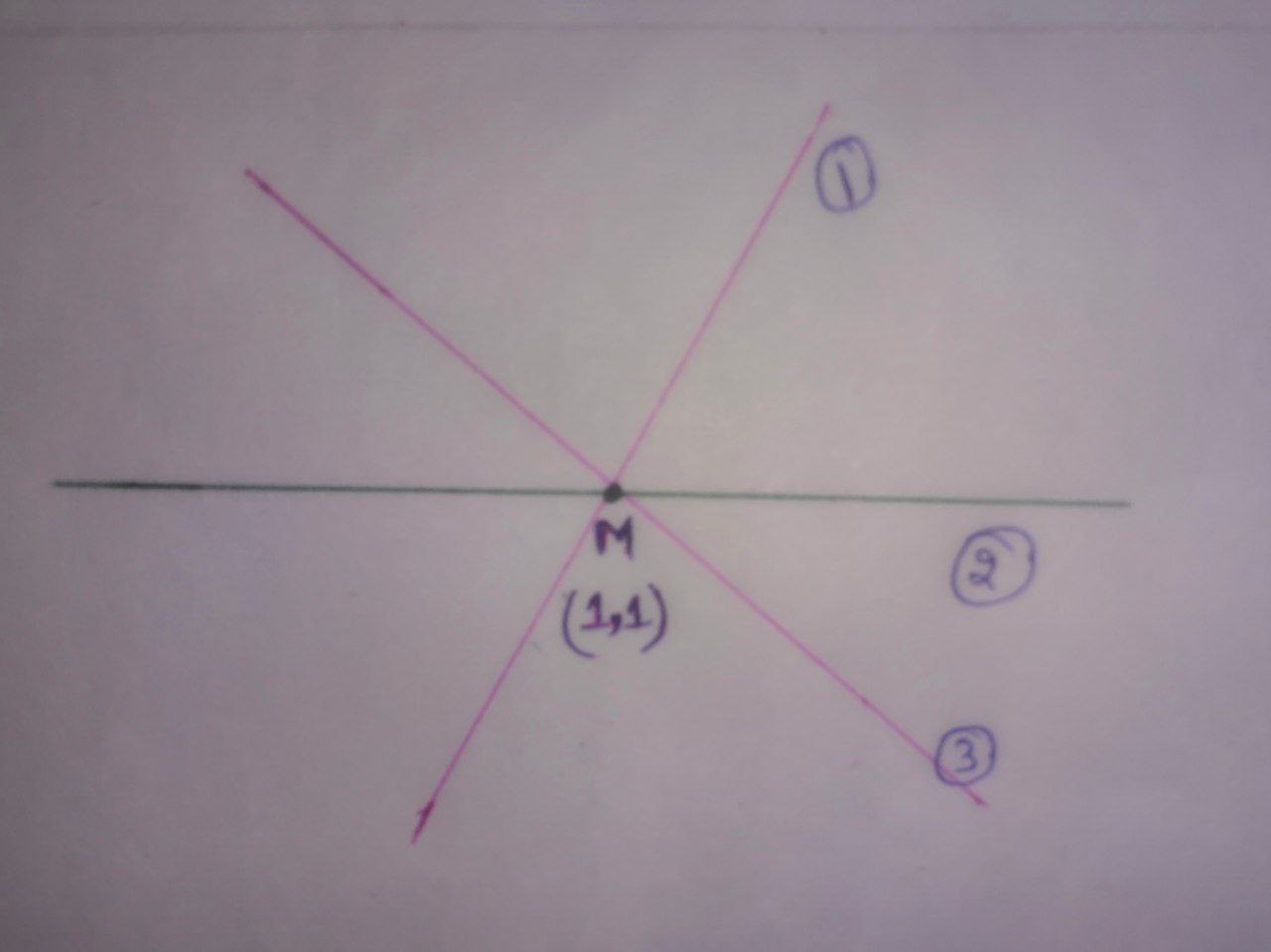
$\therefore$ These three lines are coincident.
Correct Answer $;\text{D}$