From the question, we can draw the following diagram:
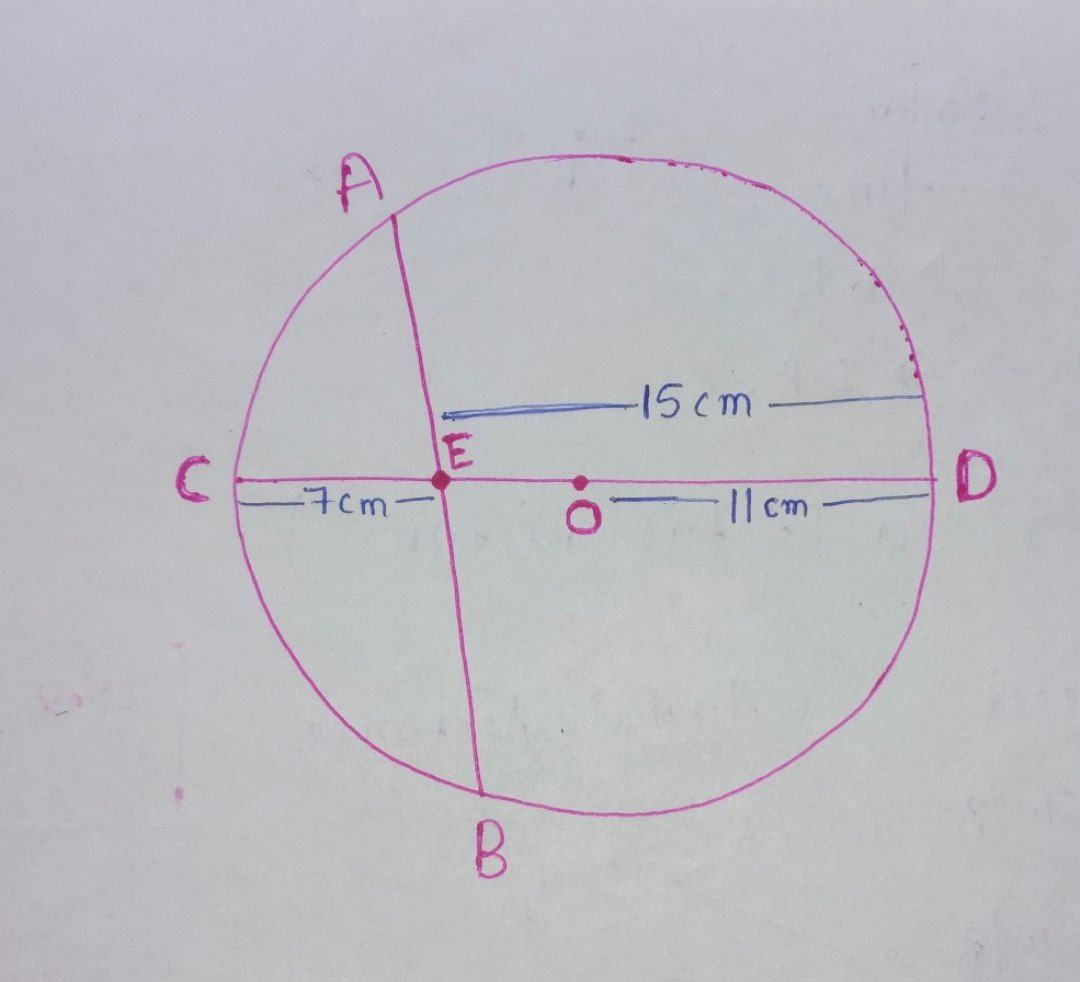
Given that,
Radius of a circle $ = 11 \; \text{cm} $
$ \text{CD}$ is a diameter $ = 11 \times 2 = 22 \; \text{cm} $
$ \text{AB}$ is a chord of length $ = 20.5 \; \text{cm} $
$ \text{AB}$ and $\text{CD}$ intersect at point $\text{E}$ inside the circle.
$ \text{CE}$ length $ = 7 \; \text{cm} $
The length of $\text{ED} = \text{CD} – \text{CE} = 22-7 = 15\;\text{cm}$
$ \text{AE} + \text{BE} = 20.5 \; \text{cm} \quad \longrightarrow (1) $
We know that, when two chords intersect AEch other inside a circle, the products of their segments are equal.
$ \boxed{\text{AE} \times \text{BE} = \text{CE} \times \text{ED}} $
$ \Rightarrow \text{AE} \times \text{BE} = 7 \times 15$
$ \Rightarrow \text{AE} \times \text{BE} = 105 \quad \longrightarrow (2) $
Let $x$ be the length of $\text{AE}.$
We have, $\text{AE + BE = AB}$
$\Rightarrow x + \text{BE} = 22.5$
$\Rightarrow \text{BE} = 22.5-x$
From the equation $(2),$ we get,
$x(22.5-x) = 105$
$\Rightarrow 22.5x – x^{2} = 105$
$\Rightarrow – x^{2} + 22.5x -105 = 0$
$\Rightarrow x^{2} - 22.5x + 105 = 0$
$\Rightarrow x^{2} - 10.5x – 10x + 105 = 0$
$\Rightarrow x(x – 10.5) – 10(x – 10.5) = 0$
$\Rightarrow (x-10.5)(x-10) = 0$
$\Rightarrow x = 10,10.5$
Thus, if $\text{AE} = 10,$ then $\text{BE} = 10.5$ and vice versa.
$ \therefore$ The difference of the lengths of $\text{BE}$ and $ \text{AE} = 10.5 – 10 = .5 \; \text{cm}.$
Correct Answer $: \text{C}$
Reference: https://brilliant.org/wiki/circles/