We can draw the rectangular axes of coordinates,
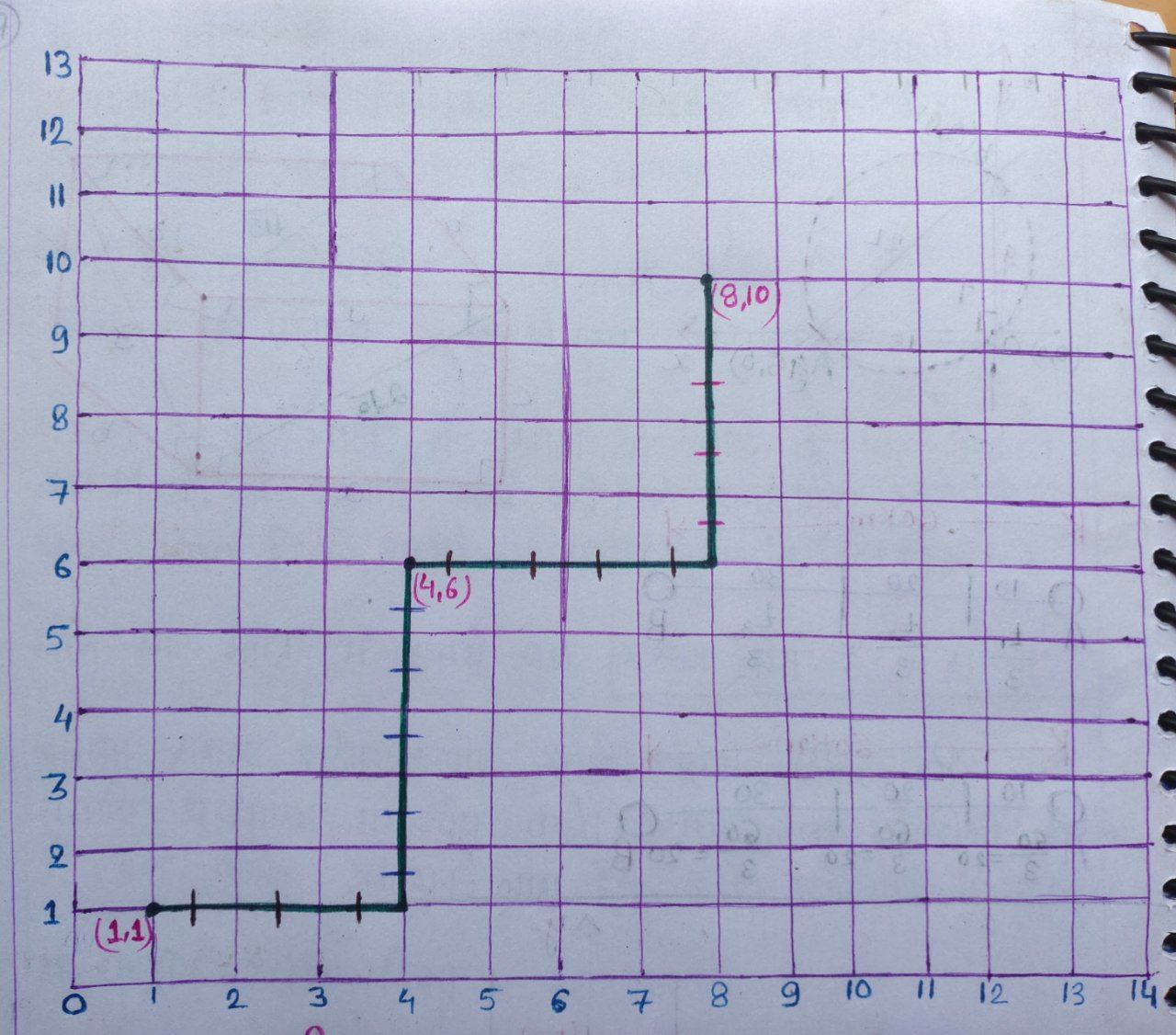
We have, each step path from any point $(x,y)$ is either to $(x, y+1)$ or to $(x+1, y)$
That mean, the path will either go along the $x$-axis or $y$-axis.
To reach from $(1,1)$ to $(4,6),$ we need,
- $3$ steps of $x$
- $5$ steps of $y$
$ \underbrace{x\;x\;x \; y\;y\;y\;y\;y}_{\qquad \text{In any order}\\ \text{(we can use permutation)}}$ (This is one possible path)
So, possible paths from $(1,1)$ to $(4,6) = \frac{8!}{3! \cdot 5!} = \frac{8 \times 7 \times 6 \times 5!}{ 3 \times 2 \times 1 \times 5!} = 56 \; \text{ways.}$
Similarly, from $(4,6)$ to $(8,10),$ we need
- $4$ steps of $x$
- $4$ steps of $y$
$ \underbrace{x\;x\;x \;x \; y\;y\;y\;y\;y}_{\qquad \text{In any order}\\ \text{(we can use permutation)}}$ (This is one possible path)
So, possible paths from $(4,6)$ to $(8,10) = \frac{8!}{4!4!} = \frac{8 \times 7 \times 6 \times 5 \times 4!}{ 4 \times 3 \times 2 \times 1 \times 4!} = 70 \; \text{ways.}$
Now, the total number of paths from $(1,1)$ to $(8,10) = 56 \times 70 = 3920 \; \text{ways.}$
$\therefore$ The total number of paths from $(1,1)$ to $(8,10)$ via $(4,6)$ is $3920.$
Correct Answer $:3920$