Given that, one can use three different transports which move at $10,20, \text{and} \; 30 \; \text{kmph}$, respectively.
- Let the total distance be LCM of $10,20,30.$
- Total distance $= \text{LCM} \; (10,20,30) = 60 \; \text{km}.$
To reach from $\text{A}$ to $\text{B}$, Amal took each mode of transport $\frac{1}{3}$ of his total journey time.
Let $`\;t_{1}\text{’}$ hours be the total time taken by Amal.

We know that, $ \boxed{\text{Distance} = \text{Speed} \times \text{Time}} $
Here$,\;10 \times \left(\frac{t_1}{3} \right) + 20 \times \left(\frac{t_1}{3} \right) + 30 \times \left(\frac{t_1}{3} \right) = 60 $
$ \Rightarrow 10 \left[ \frac{t_1}{3} + \frac{2t_1}{3} + \frac{3t_1}{3} \right] = 60 $
$ \Rightarrow \frac{6t_1}{3} = 6 $
$ \Rightarrow \boxed{t_1 = 3 \; \text{hours}}$
To reach from $\text{A}$ to $\text{B},$ Bimal took each mode of transport $\frac{1}{3}$ of the total distance.
Let $`\;t_{2}\text{’}$ hours be the total time taken by Bimal.
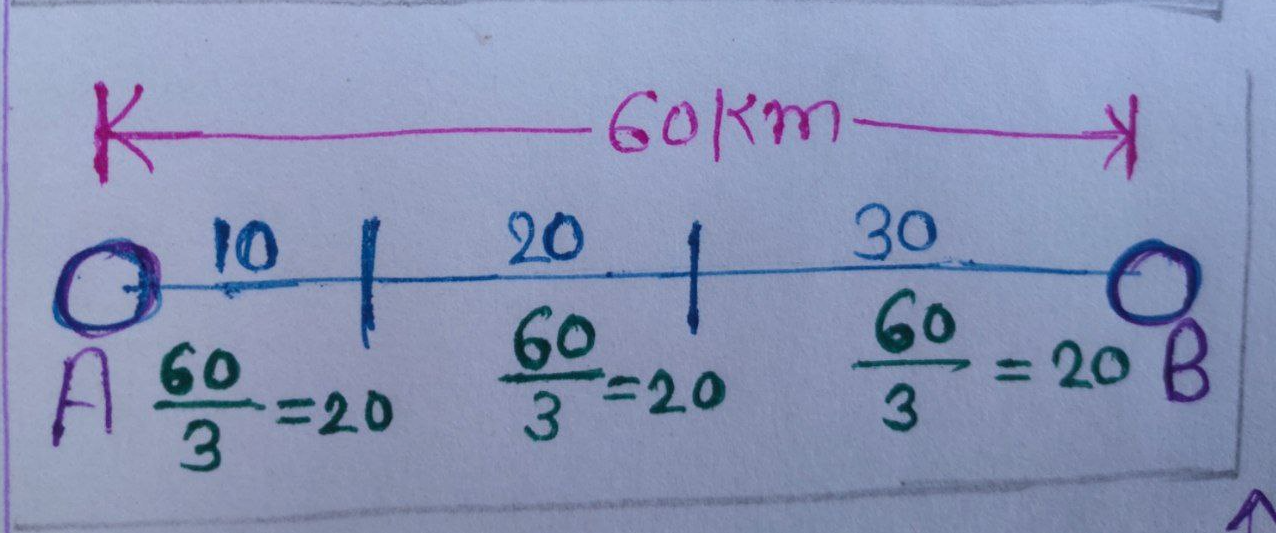
Here, total time $t_2 = \frac{20}{10} + \frac{20}{20} + \frac{20}{30}$
$ \Rightarrow t_2 = \frac {120+60+40}{60} $
$ \Rightarrow t_2 = \frac{220}{60} = \frac{22}{6} = \frac{11}{3} $
$ \Rightarrow t_2 = 3\frac{2}{3} = 3+\frac{2}{3} \; \text{hours}.$
Now, the percentage by which Bimal’s travel time exceeds Amal’s travel time $ = \left[ \frac{ \left(3+ \frac{2}{3}\right) – 3} {3} \right] \times 100\% $
$ \qquad = \left( \frac{\frac{2}{3}}{3} \right) \times 100 \%$
$ \qquad = \frac{2}{9} \times 100\% $
$ \qquad = 22 \cdot 22 \% $
$\therefore$ The percentage by which Bimal’s travel time exceeds Amal’s travel time is nearest to $22 \%.$
Correct Answer $: \text{B}$