$5^{th}$ option must be the right one.
Here is the diagram of square $ABCD$
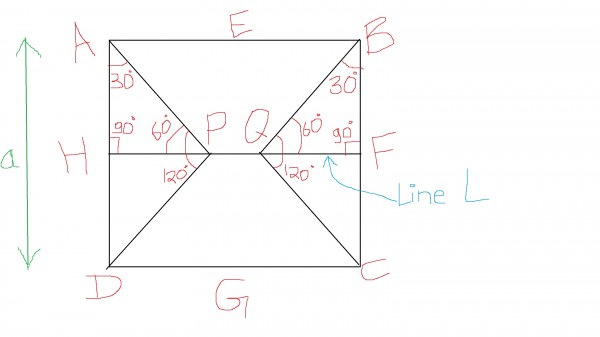
Consider the side length of the square be $a$ units.
Then $AH = BF = \frac{a}{2}$
From the rectangle $ABFH$,
$\angle AHP = \angle BFQ = 90^{\circ}.$
Now since $HF$ is the perpendicular bisector of $DA$ and $BC$,
$\angle APH = \frac{1}{2}\angle APD = 60^{\circ}$ and
$\angle BQF = \frac{1}{2}\angle BQC = 60^{\circ}$.
Hence $\angle PAH = \angle QBF = 30^{\circ}.$
Area of $\Delta APD =$ Area of $\Delta BQC = 2\left ( \frac{1}{2}\times \frac{a}{2} \times \frac{a}{2} \tan\left ( 30^{\circ} \right ) \right ) $
The area of region $ABQCDP$ = Area of square $ABCD - $ (Area of triangle $APD$ $+$ Area of triangle $BQC$).
so area of the region $ABQCDP$
$= a^{2} - \left ( 2\left ( \frac{1}{2}\times \frac{a}{2} \times \frac{a}{2} \tan\left ( 30^{\circ} \right ) \right ) + 2\left ( \frac{1}{2}\times \frac{a}{2} \times \frac{a}{2} \tan\left ( 30^{\circ} \right ) \right ) \right )$
$= a^{2} - \left ( \frac{a^{2}}{2\sqrt3}\right ). $
$= a^{2}\left ( 1 - \frac{1}{2\sqrt3} \right )$
Area of the region left after removing the area of $ABQCDP$
$= a^{2} - a^{2}\left ( 1 - \frac{1}{2\sqrt3} \right ) =\frac{a^{2}}{2\sqrt3} $.
Hence the required ratio $= \frac{a^{2}\left ( 1 - \frac{1}{2\sqrt3} \right )}{\frac{a^{2}}{2\sqrt3}}.$
On simplifying, this will give $\left ( 2\sqrt3 - 1 \right ).$