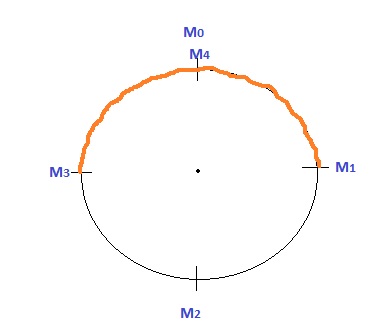
OR
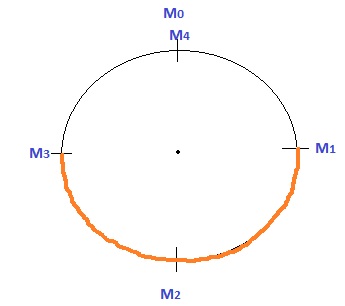
We need to find the red marked line's distance of the above picture.
Now, the circumference of the circular course $2\pi r\hspace {0.2cm} i.e.\hspace{0.2cm}2\times\dfrac{22}{7}\times{7} = 44 cm $
We're divided this circular course in $4$ equal halves.So, every half is exactly $\dfrac{44}{4}=11 km\hspace{0.1cm} long$
Or, we can say that $\color{blue}{M_{0}\Rightarrow M_{1}= 11km}$ & $\color{blue}{M_{1}\Rightarrow M_{2}= 11km}$ & $\color{blue}{M_{2}\Rightarrow M_{3}= 11km}$ & $\color{blue}{M_{3}\Rightarrow M_{4} \text{ or } M_{0}= 11km}$
$\color{green}{\text{So,The shortest distance between}}$ $\color{red}{M_{1}}$ $\color{green}{\&}$ $\color{red}{M_{3}}$ $\color{green}{\text{along the course is}}$ $\color{orange}{11+11=22\hspace{0.1cm}km}$ $\qquad\color{lightblue}{\big[∵M_{1}\rightarrow M_{3}= M_{1}\rightarrow M_{2}+M_{2}\rightarrow M_{3}\hspace{0.2cm}OR\hspace{0.2cm} M_{1}\rightarrow M_{3}= M_{1}\rightarrow M_{0}+M_{0}\rightarrow M_{3}\hspace{0.2cm} \big]}$