The adjoining figure shows a set of concentric squares.
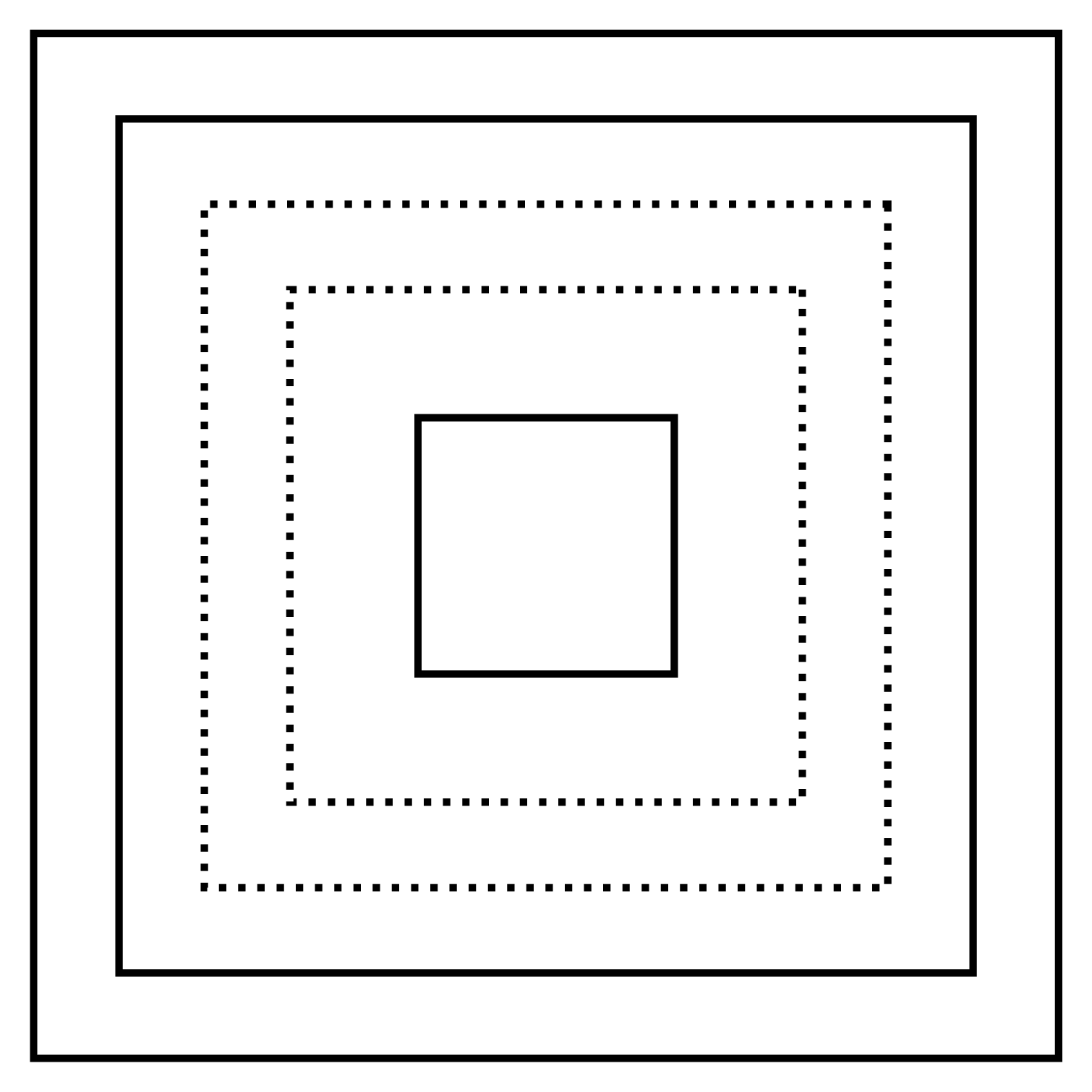
If the diagonal of the innermost square is $2$ units, and if the distance between the corresponding corners of any two successive squares is $1$ unit, find the difference between the areas of the eighth and the seventh square, counting from the innermost square.
- $10^{2}$
- $30$
- $35^{2}$
- None of these