CAT 1999 | Question: 105

Question

Answer the question based on the following information.

A road network (shown in the figure below) connects cities A, B, C and D. All road segments are straight lines. D is the mid-point on the road connecting A and C. Roads AB and BC are at right angles to each other with BC shorter than AB. The segment AB is $\text{100 km}$ long.

Ms X and Mr Y leave A at $\text{8.00 a.m.,}$ take different routes to city C and reach at the same time. X takes the highway from A to B to C and travels at an average speed of $\text{61.875 kmph.}$ Y takes the direct route AC and travels at $\text{45 kmph}$ on segment AD. Y’s speed on segment DC is $\text{55 kmph.}$

What is the length of the road segment BD?

• A. $\text{50 km}$
• B. $\text{52.5 km}$
• C. $\text{55 km}$
• D. Cannot be determined

Answer 1

There is a theroem that "Mid point of hypotenous is equidistance from all vertices . "
So D is equidistance from A, B,C . 
 

Given AB =100 KM , let BC =x km ; (where x < 100 [given] )

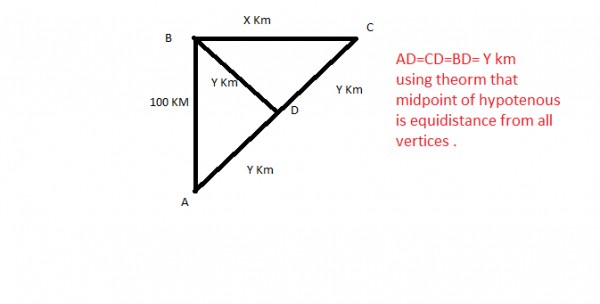
So using pythagorous theorem . 

(2y)^2=(100)^2+(x)^2    ................................... (i)

As both B and C reach at the last point at the same time . so 
(100+x)/ 61.875 = y/45 + y/55    ................................. (ii)

 

By solving equation (i) and (ii)  . ...
x= 2.5 (y) -100 
y = 169.99 and 52.31

so if y =169.99 then x =2.5(169.99)-100=324.975 (which is much larger than 100 . so this choice of y is out .)

y = 52.31 is satisfying all criteria . 
as BD =y =52.31 

So option (B) is correct .