Answer the question based on the following information.
A road network (shown in the figure below) connects cities A, B, C and D. All road segments are straight lines. D is the mid-point on the road connecting A and C. Roads AB and BC are at right angles to each other with BC shorter than AB. The segment AB is $100 \; \text{km}$ long.
Ms X and Mr Y leave A at $8.00 \; \text{a.m.,}$ take different routes to city C and reach at the same time. X takes the highway from A to B to C and travels at an average speed of $61.875$ kmph. Y takes the direct route AC and travels at $45$ kmph on segment AD. Y’s speed on segment DC is $55$ kmph.
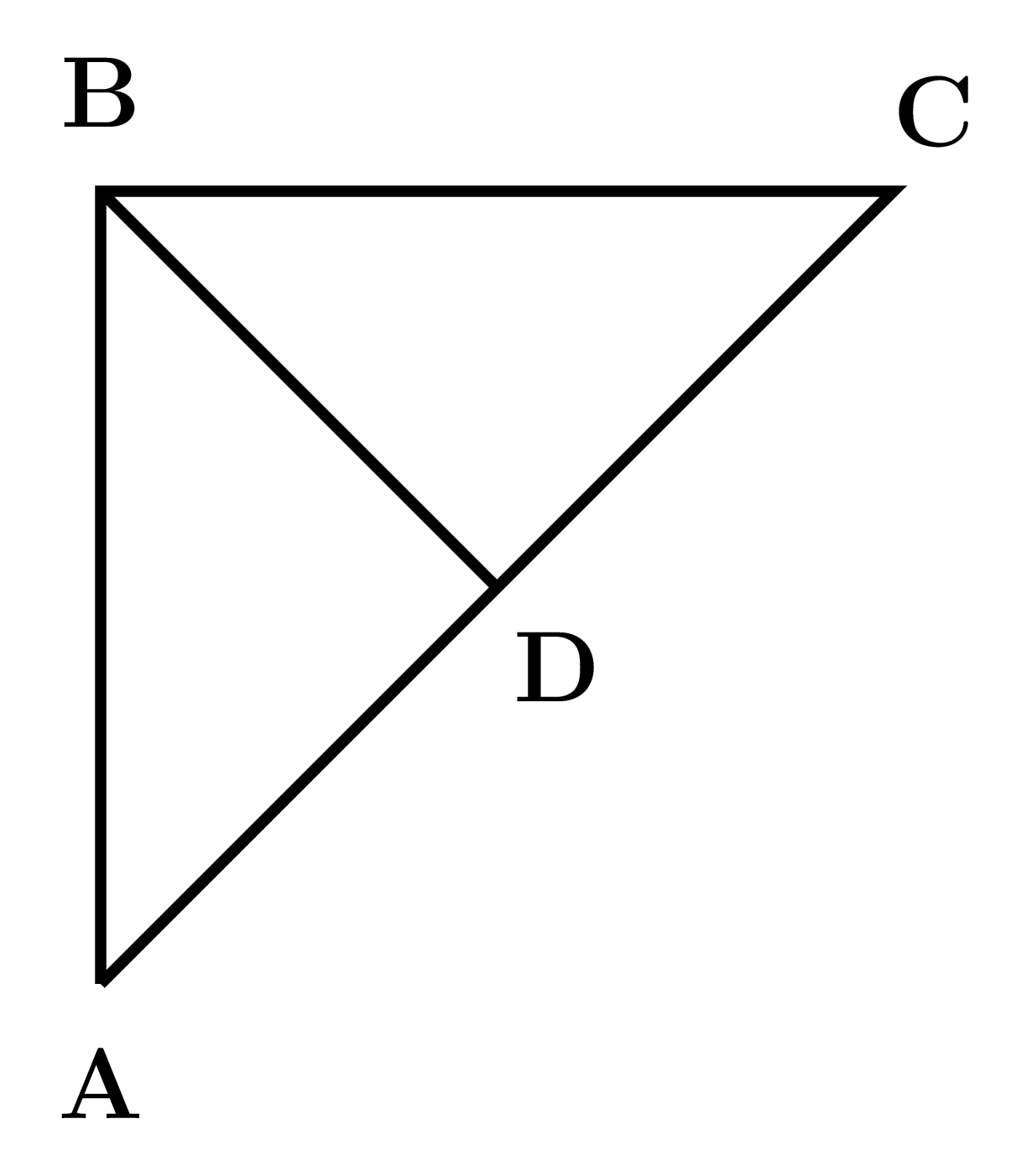
What is the average speed of Y?
- $47.5$ kmph
- $49.5$ kmph
- $50$ kmph
- $52$ kmph