Answer the question on the basis on the basis of the information given below.
Consider three circular parks of equal size with centres at $A_1,\:\: A_2,\:\:$ and $A_3$ respectively. The parks touch each other at the edge as shown in the figure (not drawn to scale). There are three paths formed by the triangles $A_1, \: A_2, \: A_3,\: B_1, \: B_2, \: B_3$, and $C_1, \: C_2, \: C_3,$ as shown. Three sprinters A, B, and C begin running from points $A_1,\: B_1$ and $C_1$ respectively. Each sprinter traverses her respective triangular path clockwise and returns to her starting point.
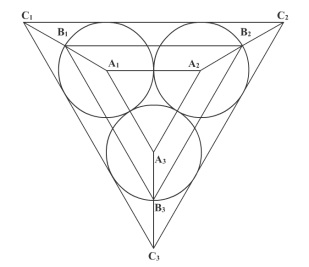
Sprinters A, B and C traverse their respective paths at uniform speeds u, v and w respectively. It is known that $u^2.v^2.w^2$ is equal to Area A: Area B: Area C, where Area A, Area B and Area C are the areas of triangles $A_1 \: A_2 \: A_3, B_1 B_2 B_3$, and $C_1\: C_2 \: C_3$, respectively. Where would A and C be when B reaches point $B_3$?
- $A_2, \: C_3$
- $A_3, \: C_3$
- $A_3, \: C_2$
- Somewhere between $A_2$ and $A_3$, Somewhere between $C_3$ and $C_1$