Answer the question on the basis of the information given below:
In the adjoining figure, I and II are circles with centres P and Q respectively. The two circles touch each other and have a common tangent that touches them at points R and S respectively. This common tangent meets the line P and Q at O. The diameters of I and II are in the ratio $4:3.$ It is also known that the length of PO is $28$ cm.
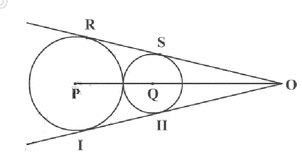
The length of SO is
- $8 \sqrt{3}$ cm
- $10 \sqrt{3}$ cm
- $12 \sqrt{3}$ cm
- $14 \sqrt{3}$ cm