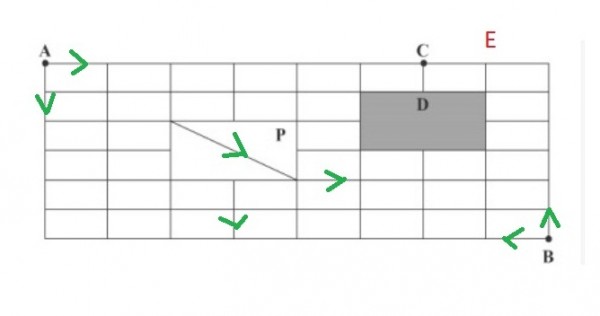
Answer $630$
from A robot can go $\text{(d,d,r,r)}$ [d=down, r=right] $ = 4!/2!2!$
then go to P line in $1$ way
then ending point of P to B $\text{(d,d,r,r,r,r)} = 6! / 4!2!$
then upwards B to E $\text{(u,u,u,u,u,u,r)} = 7! / 6!$
then E to A $1$ way
total $4! / 2!2! \times 1 \times 6! / 4!2! \times 7! / 6! \times 1 = 630$