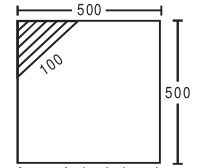
The Length of the fence(100 m) would be the hypotenuse of the right triangular area which is cordoned.You should also realize that this triangular area would be an isosceles triangle.
Thus,by pythagoras theorem the legs of the right angled isosceles triangle would be :
$100^{2}$ =2$x^{2}$
$x^{2}$=5000
$ x=50\sqrt 2 $
Area of the triangles would be given by = $ 50\sqrt 2 $ *$ 50\sqrt 2 $=2500 sq m
Hence,Option (A)2500 sq m is the correct choice.